Nuevo Proyecto 🚀
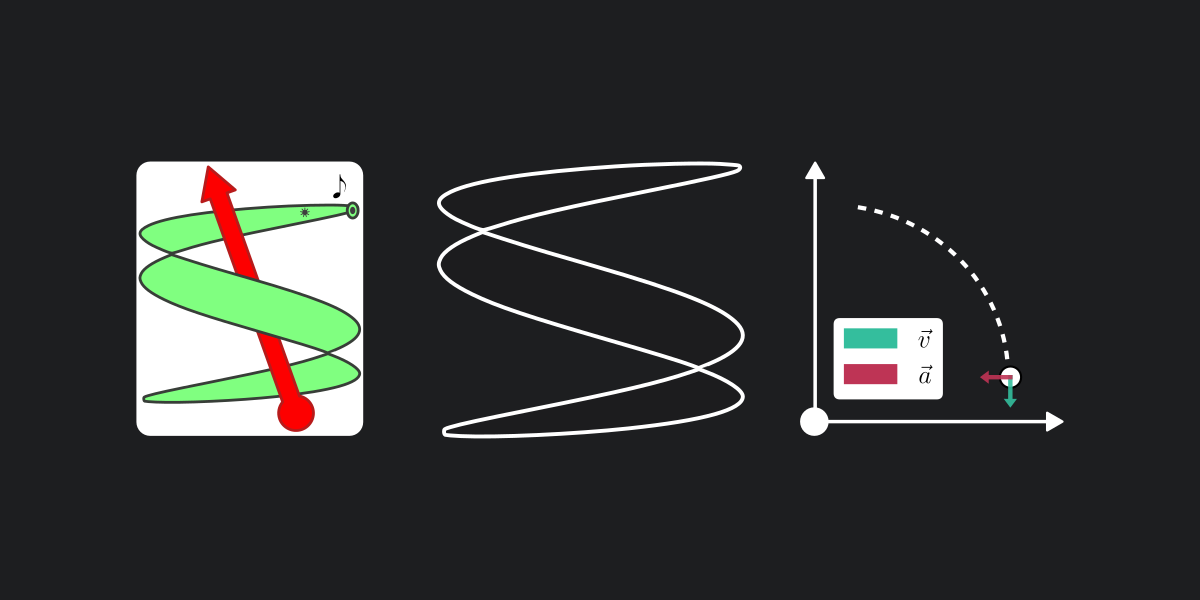
Durante un fin de semana armé este generador de animaciones de trayectorias físicas con Python. El resultado se ve así:

Cómo funciona
Para mas información recomiendo ver el GITHUB REPO. A grandes rasgos:
- Le pasamos la trayectoria.
- Creamos el vector.
- Actualizamos el gráfico según los $FPS$ de la animación.
- Renderizamos todo en un
mp4ogif.
Porqué calcular todo antes
Si calculas a medida que vas dibujando, las posiciones del objeto se van a ver bien. Pero la curva punteada va a tener saltos porque no estás calculando los puntos intermedios. Una imagen vale más que mil palabras:

La idea es que dibuje de forma suave la trayectoria, para que uno se pueda hacer una idea clara de por donde paso el objeto anteriormente.
Si calculas por frame te quedas solo con partes de la trayectoria que justo caen en el frame.
Cómo hacerlo a “tiempo real”
En el mundo MP4
Las trayectorias se dibujan a partir de las listas $t$, $x$ e $y$. $t$ tiene el instante que le corresponde a cada coordenada. En este proyecto asumo que $t$ viene de a pasos específicos. Por ej.:
$$ t = [0,0.01,0.02,0.01…, 1] $$
En este caso $t$ va de $0$ a $1$ con pasos fijos $\Delta t = 0.01$. Para mostrarlos en video a tiempo real, es necesario graficar en pasos $\Delta t = {1 \over FPS}$. Donde $FPS$ son los cuadros por minuto. Típicamente, $24$ o $30$ son suficientes. Pero si uno quiere más realismo y tiene una pantalla que lo soporta, puede subirlo más todavía. Si actualizamos el tiempo a medida que la pantalla actualiza la imagen, tenemos una relación más cercana al $1:1$ entre lo que vemos y las velocidades reales que tendría una trayectoria.
En el mundo GIF
Los GIF tienen un par de limitaciones respecto a los $FPS$. Este post tiene un poco de información al respecto. Pero para hacerlas tiempo real es necesario usar en la configuración de diSimula algunos de estos valores de $FPS$: $8.33$, $12.5$, $16.6$, $25$, $33.3$.
Unidades
Con lo mencionado antes. Se supone siempre que $t$ viene dada en segundos. Por lo que vas a tener que ajustar tus parámetros para que las unidades funcionen bien. Es un poco de trabajo extra, pero te permite formar una intuición más clara de que tan rápida es una determinada velocidad o frecuencia.
Por otro lado, las unidades de distancia de los ejes van a ser las que tengan tu función de trayectoria. Procura tener tus velocidades en unidades del tipo $\text{tus unidades de distancia} \over \text{segundos}$.
✨ Nuevo: Soporte para multiples trajectorias

Más ejemplos en la galería.
Disfrute 💌