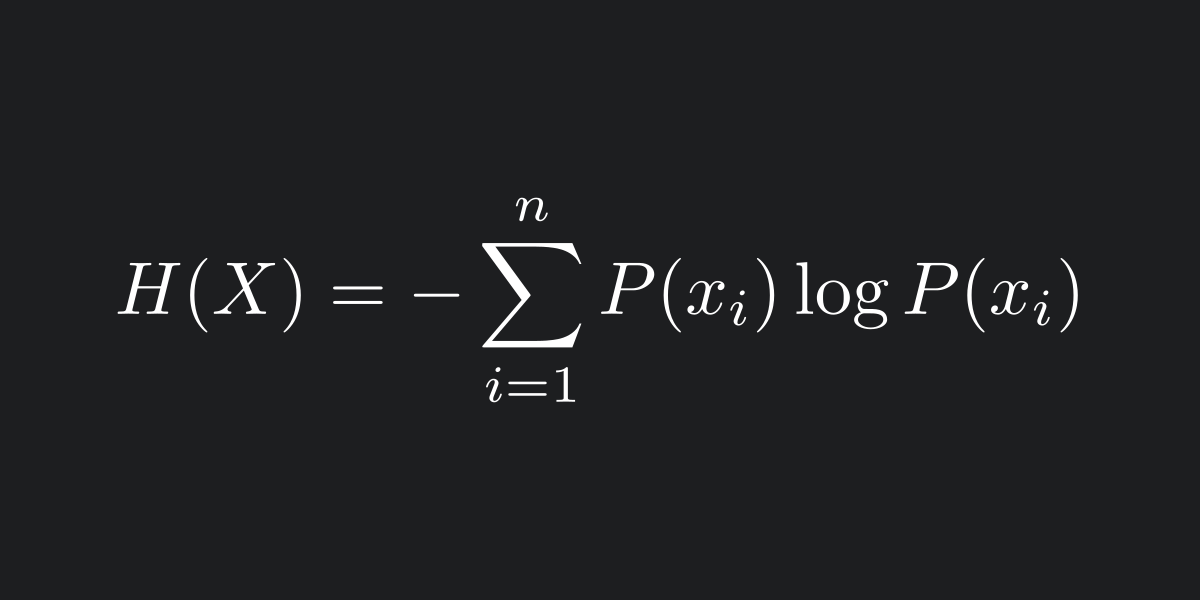Durante mi cursada de teoría de información escribí apuntes y otro material que se encuentra en este repositorio. Lo que sigue es un port al sitio de la hoja de formulas que se encuentra completa en PDF en el repositorio.
Notación de los bullet points
\( \textcolor{red}{\mathbf{>}} \ PROPIEDAD, \) \( \textcolor{red}{\#} \ DEFINICIÓN, \) \( \textcolor{red}{\bullet} \ TEMA, \) \( \textcolor{red}{\color{red}{\boldsymbol{\sim}}} \ OBSERVACIÓN, \) \( \textcolor{red}{\color{red}{\boldsymbol{*}}} \ EJEMPLO, \) \( \textcolor{red}{\color{red}{\boldsymbol{|}}} \ ALGORITMO \)
\( \textcolor{red}{\bullet}\) Matemáticas: $$ \begin{aligned} &\lim_{p \rightarrow 0} p \log (p)=0, \sum_{k=0}^{n} a r^{k}=a\left(\frac{1-r^{n+1}}{1-r}\right), \sum_{n=1}^{\infty} n r^{n} =\frac{r}{(1-r)^{2}} \\ &\sum_{k=k_1}^{k_2} ar^k =a \frac{r^{k_1} - r^{k_2 + 1}}{1-r}, \int_{a}^{b} x^n f(kx) dx = \frac{1}{k^{n+1}} \int_{ka}^{kb} u f(u) du \\ &\int_{\mathbb{R}} e^{- (ax^2 + bx + c )} = \sqrt{\frac{\pi}{a}} e^{ ( \frac{b^2}{4a} - c )} , \delta (p -p’) = \frac{1}{2\pi} \int_{\mathbb{R}} e^{i(p-p’)\xi} d\xi \end{aligned} $$
\( \textcolor{red}{\mathbf{>}}\) La truca para estas
$$ \begin{aligned} &I = \int_{ a}^{b} x^{n} e^{ \pm \alpha x} d x , { \partial_{ \alpha} e^{\pm \alpha x} = (\pm 1) x e^{t \alpha x}} , { \partial_{\alpha}^{n} e^{\pm \alpha x} = (\pm 1)^{n} x^{n} e^{\pm \alpha x}} \\ & I = (\pm 1)^{n} \partial_{\alpha}^{n} \int_{a}^{b} e^{ \pm \alpha x} d x \Rightarrow I = \left. (\pm 1)^{n+1} \partial_{\alpha}^{n} { \frac{e^{ \pm \alpha x}}{\alpha}} \right|^{ b}_{a} \\ \end{aligned} $$
$$ \begin{aligned} &\Rightarrow { \int_{ 0 }^{ \infty } x^{ n } e^{ - x / a } d x = n ! a^{ n + 1 } } , \ { \int_{ 0 }^{ \infty } x^{ 2 n + 1 } e^{ - x^{ 2 } / a^{ 2 } } d x = \frac { n ! } { 2 } a^{ 2 n + 2 } } \\ & \int_{ 0 }^{ \infty } x^{ 2 n } e^{ - x^{ 2 } / a^{ 2 } } d x = (-1)^n \sqrt { \pi } \partial_\alpha^n (\alpha^{-1/2}) \\ & \textbf{Otra:} \int_0^t e^{\alpha \varepsilon} d \varepsilon = \frac{1}{\alpha} (e^{\alpha t} - 1) \\ \end{aligned} $$
Distribución de Cauchy:
$$ f\left(x ; x_{0}, \gamma\right)=\frac{1}{\pi \gamma\left[1+\left(\frac{x-x_{0}}{\gamma}\right)^{2}\right]} , {\quad}^{x_0: \text{ ancho}}_{g:\text{ ancho a mitad de altura}} $$
\( \textcolor{red}{\bullet}\) Probabilidades: \(A: \text{event }A, \quad \bar{A}: \text{Not event }A\)
\( \textcolor{red}{\mathbf{>}}\) \(P(A)+P(\bar{A})=1\)
\( \textcolor{red}{\mathbf{>}}\) \(P(A \cup B)=P(A)+P(B)-P(A \cap B)\) (A or B)
\( \textcolor{red}{\mathbf{>}}\) \(P(A, B)=P(A \cap B)=P(A \mid B) P(B)\) (A and B)
\( \textcolor{red}{\mathbf{>}}\) \(P\left(E_{i} \mid E\right)=\frac{P\left(E_{i}\right) P\left(E \mid E_{i}\right)}{\sum_{j=1}^{k} P\left(E \mid E_{j}\right) P\left(E_{j}\right)}\) (Baye’s Formula)
\( \textcolor{red}{\mathbf{>}}\) \(P(A \mid B)=P(A)\) (Independent Trials)
\( \textcolor{red}{\mathbf{>}}\)
\(E[X] =\langle x \rangle = \int_\mathbb{R} x p(x) dx\) (continuo)
\(E[X] =\langle x \rangle = \sum_{i=1}^k x_i p_i\) (discreto)
\( \textcolor{red}{\mathbf{>}}\)
\(\operatorname{Var}(X) =E\left[(X-E[X])^{2}\right]\) $$ \begin{aligned} \operatorname{Var}(X) &=E\left[X^{2}-2 X E[X]+E[X]^{2}\right] \\ &=E\left[X^{2}\right] - 2 E[X E[X] ] +E[X]^{2} \\ &=E\left[X^{2}\right]-E[X]^{2} \end{aligned} $$
\( \textcolor{red}{\mathbf{>}}\) Probability of one of \(k\) mutually exclusive events
\( P=P\left(E_{1}\right)+P\left(E_{2}\right)+\ldots+P\left(E_{k}\right) \)
\( \textcolor{red}{\mathbf{>}}\) Total Probability, \(k\) mutually exclusive events: $$ \begin{aligned} P(E)&=P\left(E \mid E_{1}\right) P\left(E_{1}\right)+\ldots+P\left(E \mid E_{k}\right) P\left(E_{k}\right)\\ &=\sum_{i=1}^{k} P\left(E \mid E_{i}\right) P\left(E_{i}\right) \end{aligned} $$
\( \textcolor{red}{\mathbf{>}}\) Variable change, prob. density functions: $$ g(\vec{y}) = f(\vec{x}) \left| { \det \left(\frac{d\vec{x}}{d\vec{y}}\right) } \right| $$
Entropía
\( \textcolor{red}{\bullet}\) Notación:
\(\mathcal{A}_X : \text{Alfabeto de la variable aleatoria} X\)
\(p_i: \text{Probabilidades}\)
\( l_i: {\quad}^{\# \text{ de preguntas necesarias para }}_{\text{llegar al elemento} i \text{del alfabeto}} \)
\(H: \text{Entropía} \)
\(C(x):\) palabra clave asociada a \(x .\)
\(\ell(x):\) longitud de \(C(x)\), medida en dígitos.
\( \textcolor{red}{\#}\)
Num. medio de preguntas en pie de igualdad: $$ \left\langle \begin{array}{c} \# \text { preguntas en pie de igualdad} \\ \text { bien elegidas } \end{array} \right\rangle=\sum_{i} p_{i} \ell_{i} $$
Usando: \( p_{i} = D^{- \ell_{i}} \Leftrightarrow \ell_{i}=-\log_{D} p_{i} \)
$$ \text{Se tiene: } \left\langle\begin{array}{c} \# \text { preguntas } \\ \text { bien elegidas } \end{array}\right\rangle=-\sum_{i} p_{i} \log_{D} p_{i} $$
\( \textcolor{red}{\#}\) Entropía: $$ H=-\sum_{i} p_{i} \log_{D} p_{i} $$
\( \textcolor{red}{\mathbf{>}}\) Conversión de unidades: $$ H_{D}=-\sum p_{i} \log_{D} p_{i}=-\sum p_{i} \frac{\log_{D^{\prime}}\left(p_{i}\right)}{\log_{D^{\prime}}(D)}=\frac{1}{\log_{D^{\prime}}(D)} H_{D^{\prime}} $$
\( \textcolor{red}{\bullet}\) Propiedades de \(H\):
\( \textcolor{red}{\mathbf{>}}\) Anidación: Si \(Y=f(X)\), \( {\mathcal{C}(y) \subset \mathcal{A}_{X}} \) contiene a todo \(x:x \stackrel{f}{\rightarrow} y\) \(\Rightarrow\)
$$ H(X)=H(Y)-\sum_{y} p(y) \sum_{x \in C(y)} p(x \mid y) \log [p(x \mid y) $$
\( \textcolor{red}{\mathbf{>}}\) Cotas y sus implicaciones:
$$\underbrace{0}_{\text{Determinista}}\leq H(X) \leq \underbrace{ \log \vert A_X \vert}_{\text{Uniforme}}$$
\( \textcolor{red}{\bullet}\) Caso bivariado: Con \(\mathbf{X}=\left(X, Y\right)\) variable aleatoria bivariada, \(\mathbf{X}\) \(\in\) \(A_{X}\) \(\times\) \(A_{Y}\) con prob. conjunta \(p\left(x, y\right)\)
\( \textcolor{red}{\#}\) Entropía conjunta: $$ H\left(X_{1}, X_{2}\right)=-\sum_{x_{1}} \sum_{x_{2}} p\left(x_{1}, x_{2}\right) \log_{D}\left[p\left(x_{1}, x_{2}\right)\right] $$
\( \textcolor{red}{\#}\) Entropías marginales(una a una): $$ \begin{aligned} H\left(X_{1}\right)&=-\sum_{x_{1}} p\left(x_{1}\right) \log_{D}\left[p\left(x_{1}\right)\right] \\ H\left(X_{2}\right)&=-\sum_{x_{2}} p\left(x_{2}\right) \log_{D}\left[p\left(x_{2}\right)\right] \\ &\text{distr. marginales } \\ p\left(x_{1}\right)&=\sum_{x_{2}} p\left(x_{1}, x_{2}\right), p\left(x_{2}\right)=\sum_{x_{1}} p\left(x_{1}, x_{2}\right) \end{aligned} $$
\( \textcolor{red}{\#}\) Entropía condicional: $$ \begin{aligned} H\left(X_{1} \mid X_{2}\right)=-\sum_{x_{2}} p\left(x_{2}\right) \sum_{x_{1}} p\left(x_{1} \mid x_{2}\right) \log_{D}\left[p\left(x_{1} \mid x_{2}\right)\right] \\ H\left(X_{2} \mid X_{1}\right)=-\sum_{x_{1}} p\left(x_{1}\right) \sum_{x_{2}} p\left(x_{2} \mid x_{1}\right) \log_{D}\left[p\left(x_{2} \mid x_{1}\right)\right] \end{aligned} $$
\( \textcolor{red}{\mathbf{>}}\) Regla de la cadena: $$ \begin{aligned} H(X, Y) &= H(X)+H(Y \mid X) \\ &= H(Y)+H(X \mid Y) \end{aligned} $$ $$ \begin{aligned} H(X, Y) &=-\sum_{x} \sum_{y} p(x, y) \log [p(x, y)] \\ &=-\sum_{x} \sum_{y} p(x) p(y \mid x) \log [p(x) p(y \mid x)] \\ \end{aligned} $$ $$ \begin{aligned} &=-\sum_{x} p(x) \sum_{y} p(y \mid x){\log [p(x)]+\log [p(y \mid x)]} \\ \end{aligned} $$
$$ = - \sum_{x} p(x) \log [p(x)] \underbrace{\sum_{y} p(y \mid x)}_{1} $$
$$ \begin{aligned} & \quad - \sum_{x} p(x) \sum_{y} p(y \mid x) \log [p(y \mid x)] \\ &=H(X)+H(Y \mid X) \end{aligned} $$
\( \textcolor{red}{\mathbf{>}}\) Regla de la cadena multivariable: $$ H\left(X_{1}, X_{2}, \ldots, X_{n}\right) = \sum_{i=1}^{n} H\left(X_{i} \mid X_{i-1}, \ldots, X_{1}\right) $$
\( \textcolor{red}{\mathbf{>}}\) Cotas \(H\) condicional:
$$ \underbrace{0}_{\text{determinista}} \leq H(X \mid Y) \leq \underbrace{H(X)}_{\text{Independientes}} \leq \underbrace{\log\vert A_X \vert}_{\text{Uniforme}} $$
\( \textcolor{red}{\mathbf{>}}\) Cotas \(H\) multivariable: $$ H\left(X_{1}, X_{2}, \ldots, X_{N}\right) \leq \sum_{i} H\left(X_{i}\right) $$
\( \textcolor{red}{\mathbf{>}}\) \(H(X|X) = H(X)\)
\( \textcolor{red}{\mathbf{>}}\) Condición de independencia: $$ \begin{aligned} X, Y \text{ son independientes} & \Leftrightarrow H(X \mid Y)=H(X) \\ X, Y \text{ son independientes} & \Leftrightarrow H(Y \mid X)=H(Y) \\ X, Y \text{ son independientes} & \Leftrightarrow H(X, Y) = H(X)+H(Y) \end{aligned} $$
\( \textcolor{red}{\mathbf{>}}\) \(H(X, Y \mid Z)=H(X \mid Z) + H(Y \mid X,Z)\)
Información mutua
\( \textcolor{red}{\#}\) Función convexa: \(f(x)\) es convexa en el intervalo \([a, b]\) \(\Leftrightarrow \forall x_{1}, x_{2} \in [a, b]\), \(\forall \lambda \in[0,1]\):
$$ \underbrace{f\left[\lambda x_{1}+(1-\lambda) x_{2}\right]}_{\text{Gráfico de } f \text{ en } x \in (x_1,x_2)} \leq \underbrace{\lambda f\left(x_{1}\right)+(1-\lambda) f\left(x_{2}\right)}_{\text{Cuerda en} x \in (x_1,x_2)} $$
\( \textcolor{red}{\#}\) Estrictamente convexa: La función es convexa y únicamente en los extremos se cumple la igualdad.
\( \textcolor{red}{\mathbf{>}}\) Si \(f’’>0(f’’>0)\) en un intervalo \(I\) \(\Rightarrow\) es estrictamente convexa (cóncava) en \(I\).
\( \textcolor{red}{\mathbf{>}}\) Desigualdad de Jansen: Si \(f: \mathbb{R} \rightarrow \mathbb{R}\) es convexa, y \(X\) es una variable aleatoria\(\Rightarrow\) $$ \langle f(X)\rangle \geq f(\langle X\rangle), \quad \forall \text{ distribución } p(x) $$
\( \textcolor{red}{\color{red}{\boldsymbol{\sim}}}\) Si \(f\) es estrictamente convexa, \(\langle f(X)\rangle = f(\langle X\rangle)\) \(\Leftrightarrow\) \(X\) es determinista.
\( \textcolor{red}{\mathbf{>}}\) Desigualdad de la suma de logaritmos: Dados \(a_{1}, \ldots, a_{n} \in\) \({\mathbb{R}^{+}}_{0}\) , \(b_{1}\), \(\ldots\), \(b_{n}\) \(\in\) \(\mathbb{R}^{+}\) $$ \sum_{i=1}^{n} a_{i} \log \left(\frac{a_{i}}{b_{i}}\right) \geq\left(\sum_{i=1}^{n} a_{i}\right) \log \left(\frac{\sum_{j=1}^{n} a_{j}}{\sum_{k=1}^{n} b_{k}}\right) $$
\( \textcolor{red}{\color{red}{\boldsymbol{\sim}}}\) \((\geq)\) se vuelve (=) \(\Leftrightarrow\) \(\frac{a_{i}}{b_{i}} = \text{cte.}\) (no depende de \(i\)).
\( \textcolor{red}{\#}\) Divergencia de Kullback-Leibler: Dadas \(p\left(x_{i}\right)\), \(q\left(x_{i}\right)\) distr. de prob. con \(x_i \in A_X, \forall i\): $$ D_{\mathrm{KL}}(p | q)=\sum_{i} p\left(x_{i}\right) \log \left[\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right] $$
\( \textcolor{red}{\bullet}\) Propiedades \(D_{KL}\):
\( \textcolor{red}{\mathbf{>}}\) \(\underbrace{0}_{p=q} \leq D_{\mathrm{KL}}(p | q)\)
\( \textcolor{red}{\mathbf{>}}\) \(D_{KL}\) es convexa
\( \textcolor{red}{\mathbf{>}}\) \(\exists\) (muchos) casos en los que:
- \( \textcolor{red}{\mathbf{>}}\) \(D_{\mathrm{KL}}(p | q) \neq D_{\mathrm{KL}}(q | p)\) (Asimetría)
- \( \textcolor{red}{\mathbf{>}}\) \(D_{\mathrm{KL}}(p | q)+D_{\mathrm{KL}}(q | r)<D_{\mathrm{KL}}(r | p)\) (Desigualdad triangular)
- \( \textcolor{red}{\mathbf{>}}\) \(D_{\mathrm{KL}}\) diverge \(=\infty\)
\( \textcolor{red}{\#}\) Información mutua: Con variables aleatorias \(X\),\(Y\) con distr. conjunta \(p(x, y)\), la info. mutua \(I(X ; Y)\) entre ellas se define como
$$ \begin{aligned} I(X ; Y) &=H(Y)-H(Y \mid X) \\ &=H(X)-H(X \mid Y) \\ &=H(X)+H(Y)-H(X, Y) \\ &=D_{\mathrm{KL}}[p(x, y) | p(x) p(y)] \\ &=\sum_{x \in{0,1}} \sum_{y \in{0,1}} p(x, y) \log \left[\frac{p(x, y)}{p(x) p(y)}\right] \end{aligned} $$
\( \textcolor{red}{\color{red}{\boldsymbol{\sim}}}\) Las dos variables se separan por ; Por ejemplo, $$ \begin{aligned} I\left(X_{1}, X_{2} ; Y_{1}, Y_{2}, Y_{3}\right) &= H\left(X_{1}, X_{2}\right) \\ & - H\left(X_{1}, X_{2} \mid Y_{1}, Y_{2}, Y_{3}\right) \end{aligned} $$
\( \textcolor{red}{\#}\) Información mutua condicionada: $$ \begin{aligned} I(X ; Y \mid Z) &=H(X \mid Z)-H(X \mid Y, Z) \\ &=H(Y \mid Z)-H(Y \mid X, Z) \\ &=H(X \mid Z)+H(Y \mid Z)-H(X, Y \mid Z) \\ &=\sum_{z} p(z) D_{\mathrm{KL}}[p(x, y \mid z) | p(x \mid z) p(y \mid z)] \end{aligned} $$ donde \(X, Y, Z\) son variables aleatorias.
\( \textcolor{red}{\#}\) \(I\) condicionada multivariada: $$ I\left(X_{1}, X_{2}, \ldots, X_{n} ; Y\right)=\sum_{i=1}^{n} I\left(X_{i} ; Y \mid X_{i-1}, X_{i-2}, \ldots, X_{1}\right) $$ $$ \left| \begin{aligned} I & \left(X_{1}, X_{2}, \ldots, X_{n} ; Y\right) = \\ \quad &=H\left(X_{1}, X_{2}, \ldots, X_{n}\right)-H\left(X_{1}, X_{2}, \ldots, X_{n} \mid Y\right) \\ \quad &=\sum_{i=1}^{n} H\left(X_{i} \mid X_{i-1}, \ldots, X_{1}\right)\\ &-\sum_{i=1}^{n} H\left(X_{i} \mid X_{i-1}, \ldots, X_{1}, Y\right) \\ \quad &=\sum_{i=1}^{n} I\left(X_{i} ; Y \mid X_{1}, X_{2}, \ldots, X_{i-1}\right) \end{aligned} \right. $$
\( \textcolor{red}{\mathbf{>}}\) \( I(X ; Y, Z)=I(X ; Y)+I(X ; Z \mid Y) \)
\( \textcolor{red}{\bullet}\) Propiedades de \(I\) mutua:
\( \textcolor{red}{\mathbf{>}}\) \(I(X)\)(y \(H(X)\))no depende de \(X\), solo de sus prob.
\( \textcolor{red}{\mathbf{>}}\) \(I(X ; X)=H(X)\) viene de \(H(X \mid X)=0\)
\( \textcolor{red}{\mathbf{>}}\) \(I(X ; Y)=I(Y ; X)\) (simetría)
\( \textcolor{red}{\mathbf{>}}\)
\(Y=f(X), f \ ^\text{funcion}_\text{inyectiva} \Rightarrow I(X ; Y)=H(X)=H(Y)\)
\( \textcolor{red}{\mathbf{>}}\) Variables aleatorias \(X, Y, Z=f(Y)\)
\(\Rightarrow\) \(I(X ; Y) \geq I(X ; Z)\)
\( \textcolor{red}{\mathbf{>}}\) Cota \(I\) mutua:
$$\underbrace{0}_{\text{independiente}}\leq I(X ; Y) \leq \underbrace{\min [H(X), H(Y)]}_{\text{determinista}} $$
para el caso uniforme
$$ \underbrace{0}_{\text{independiente}} \leq I(X ; Y) \leq \underbrace{\min \left[\log \left\vert A_{X} \right\vert, \log \left\vert A_{Y}\right\vert \right]}_{\text{uniforme}} $$
\( \textcolor{red}{\#}\) Estadística suficiente: Un mapeo \(z=f(y)\) es una estadística suficiente \(\Leftrightarrow\) \(I(X ; Y)=I(X ; Z)\).